近日，我校数学与统计学院徐玮玮教授和电子科技大学计算机科学与工程学院博士生石璐作为共同第一作者，电子科技大学计算机科学与工程学院张少帅研究员和徐玮玮教授作为共同通讯作者，在基于GPU架构的高效精确奇异值分解算法上取得重要进展，相关成果以“Towards Singular Value Decomposition for Rank-Deficient Matrices: An Efficient and Accurate Algorithm on GPU Architectures”为题，被计算机体系结构CCF A类会议PPoPP录用。

矩阵计算作为信息处理与人工智能的核心基础，被列为大数据计算"七大巨人问题"之一。矩阵计算对芯片性能（尤其是CPU、GPU、AI芯片如TPU、NPU等）有显著影响，无论在通用CPU还是专用AI芯片中，高效矩阵计算都是设计和优化的核心。在当前技术竞争背景下，通过数学算法的理论突破和软件优化来提升国产芯片实际算力，是缩小算力差距的重要路径。低秩矩阵的奇异值分解（singular value decomposition，简称SVD）在推荐系统、矩阵补全、生物信息学等领域应用广泛，但现有算法未能充分利用矩阵低秩特性，导致整体计算性能较低。如英伟达官方库cuSOLVER在H100-PCIe GPU上仅能达到0.5 TFLOPs，而GPU的峰值性能为51 TFLOPs，意味着计算低秩SVD仅能利用硬件计算能力的1%以下。

为了解决计算低秩SVD性能低的问题，论文利用了2023年Chen Xu、Weiwei Xu和Kaili Jing发表在National Science Review中的矩阵低秩分解算法-QB算法[1]，降低计算低秩矩阵SVD的算法复杂度;再针对Gram–Schmidt正交化过程中精度下降的问题，提出了利用Householder变换部分替代Gram–Schmidt正交化的方法与混合精度方法，使得最终SVD计算的精度（O(1e-07)）超过英伟达官方库的SGESVD函数（O(1e-06)）。

为了进一步提升计算性能，论文还引入了针对 GPU 架构的工程优化。首先，针对 Householder 变换中较为耗时的 panel 分解部分，使用了重建 WY 表示的 TSQR（瘦高矩阵 QR 分解），提高了 panel 分解的并行度，并降低了在 GPU 共享内存上的同步耗时。其次，针对在秩较高的情况下，SVD 较 QB 分解成为新的性能瓶颈的问题，论文提出了使用更高精度的特征值分解来求解 SVD，并理论证明了这种混合精度的 SVD 算法可以保证最终的后向误差与奇异值误差能够达到 FP32 的机器精度。这种混合精度的 SVD 算法在矩阵高秩的情况下，显著加速了 SVD 的计算速度，并具备更高的精度

实验上，论文对比了不同矩阵尺寸与秩的情况下提出的SVD算法与英伟达官方库中的SVD性能。在矩阵尺寸为26624的性能对比中，有约5-6798倍的加速。在秩为32的情况下，最大较英伟达官方库带来6798倍的加速；在秩为4096的情况下，较英伟达官方库有近100倍的加速；对于满秩矩阵，较英伟达仍有近5倍的加速。另外，该算法无需矩阵秩的信息，而是在QB分解的过程中自动揭示矩阵的秩。

最后，论文还论证了提出的方法在图像压缩领域的应用潜力：在保持压缩率与压缩质量同等的情况下，提出的算法具有更高的性能。

ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming，即 PPoPP，是由 ACM 主办的并行计算国际会议。2025 年 PPoPP 仅收录 51 篇论文，接受率为 18.3%。本次会议将于 2026 年 1 月 31 日至 2 月 4 日在澳大利亚悉尼举办，论文作者将参会并宣讲论文。

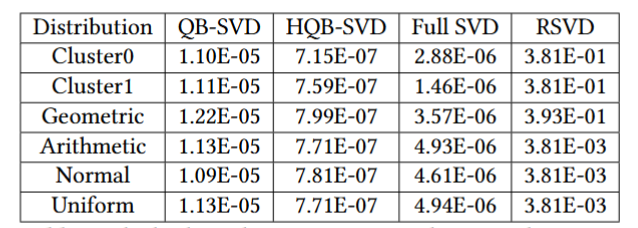
图1：论文提出方法与英伟达官方库SVD的精度对比

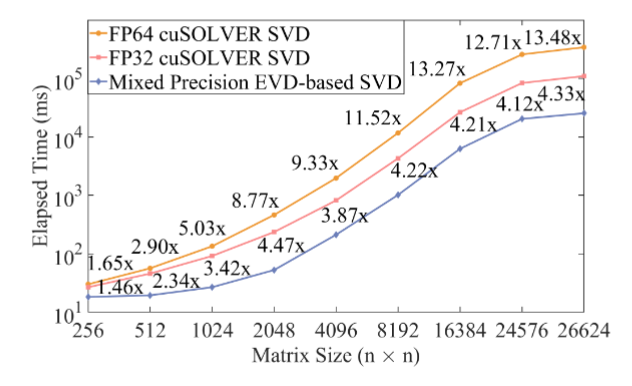
图2：混合精度SVD与英伟达官方库SVD性能对比

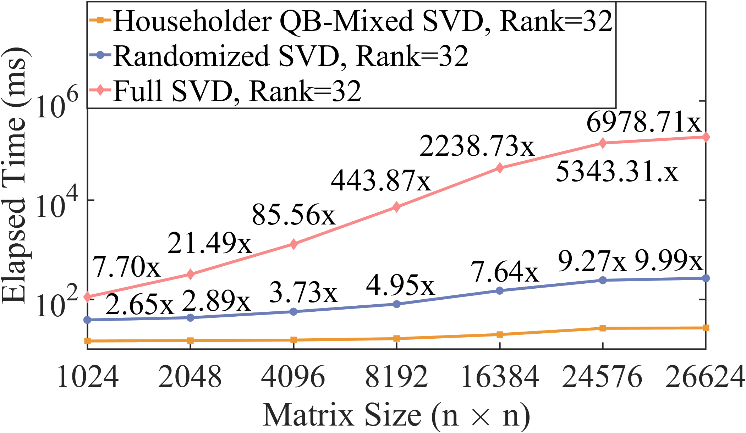
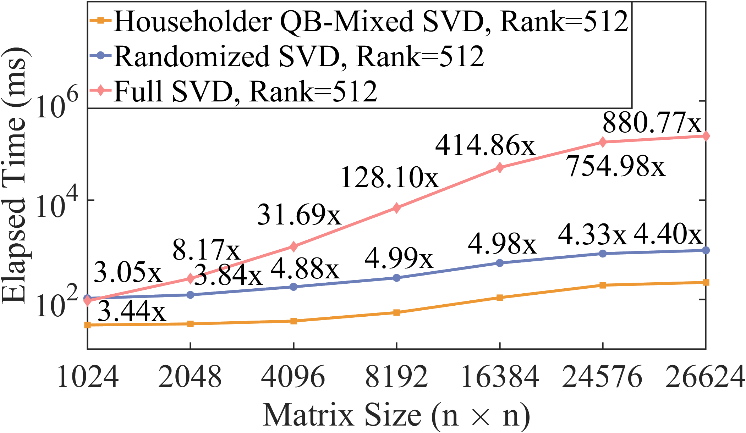
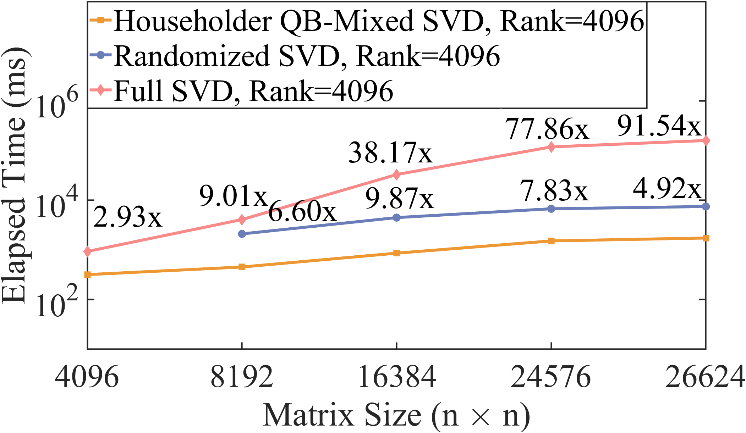
图3：最终SVD性能与英伟达官方库SVD与随机SVD性能对比

图4：在保持压缩率与压缩质量同等的情况下，提出的算法具有更高的性能

论文信息如下：

L. Shi, W.W. Xu, S.S. Zhang,Towards Singular Value Decomposition for Rank-Deficient Matrices: An Efficient and Accurate Algorithm on GPU Architectures, PPoPP 2026, https://doi.org/10.1145/3774934.3786427.